About the library
StarNEig library aims to provide a complete task-based software stack for solving dense nonsymmetric (generalized) eigenvalue problems. The library is built on top of the StarPU runtime system and targets both shared memory and distributed memory machines. Some components of the library support GPUs.
The four main components of the library are:
- Hessenberg(-triangular) reduction: A dense matrix (or a dense matrix pair) is reduced to upper Hessenberg (or Hessenberg-triangular) form.
- Schur reduction (QR/QZ algorithm): A upper Hessenberg matrix (or a Hessenberg-triangular matrix pair) is reduced to (generalized) Schur form. The (generalized) eigenvalues can be determined from the diagonal blocks.
- Eigenvalue reordering and deflating subspaces: Reorders a user-selected set of (generalized) eigenvalues to the upper left corner of an updated (generalized) Schur form.
- Computation of eigenvectors: Computes (generalized) eigenvectors for a user-selected set of (generalized) eigenvalues.
The library has been developed as a part of the NLAFET project. The project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 671633. Support has also been received from eSSENCE, a collaborative e-Science programme funded by the Swedish Government via the Swedish Research Council (VR), and VR Grant E0485301. The development and performance evaluations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at HPC2N partially funded by VR through grant agreement No. 2016-07213. The library is published under the open-source BSD 3-Clause license.
Please cite the following article when referring to StarNEig:
Mirko Myllykoski, Carl Christian Kjelgaard Mikkelsen: Task-based, GPU-accelerated and Robust Library for Solving Dense Nonsymmetric Eigenvalue Problems, Concurrency and Computation: Practice and Experience, 33 (11), 2021 (online since 2020; e5915), doi: 10.1002/cpe.5915
Performance
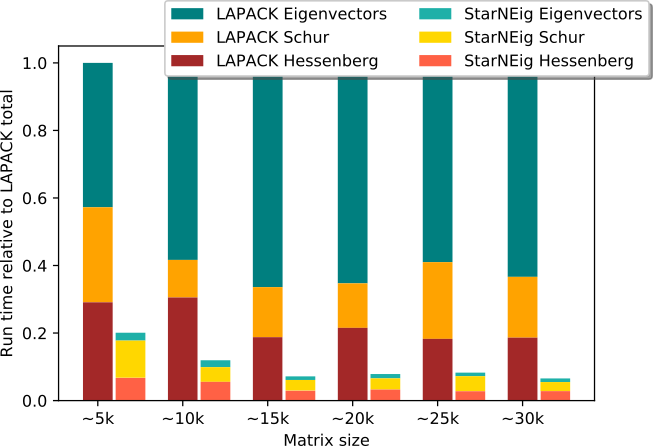
Performance comparison against LAPACK (with parallel BLAS) using 25 CPU cores and a Nvidia V100 GPU:
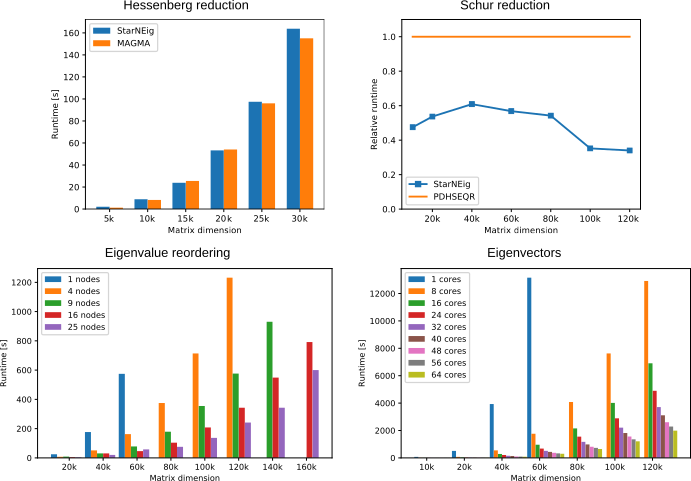
Performance comparisons against MAGMA (Nvidia V100 GPU) and ScaLAPACK (distributed memory), and strong scalability on shared and distributed memory machines:
Also, see following publications:
- Mirko Myllykoski: Algorithm 1019: A Task-based Multi-shift QR/QZ Algorithm with Aggressive Early Deflation, ACM Transactions on Mathematical Software, 48 (1), Article 11, pp. 1-36, 2022 (online since 2021), doi: 10.1145/3495005
- Mirko Myllykoski, Carl Christian Kjelgaard Mikkelsen: Task-based, GPU-accelerated and Robust Library for Solving Dense Nonsymmetric Eigenvalue Problems, Concurrency and Computation: Practice and Experience, 33 (11), 2021 (online since 2020; e5915), doi: 10.1002/cpe.5915
- Mirko Myllykoski, Carl Christian Kjelgaard Mikkelsen, Angelika Schwarz, Bo Kågström: D2.7 Eigenvalue solvers for nonsymmetric problems, public NLAFET deliverable, 2019 (download)
Current status
The stable 0.1-series currently supports only real arithmetic (real input and output matrices but real and/or complex eigenvalues and eigenvectors). In addition, some interface functions are implemented as LAPACK and ScaLAPACK wrapper functions.
Standard eigenvalue problems:
| Shared memory | Distributed memory | CUDA | |
|---|---|---|---|
| Hessenberg | Complete | ScaLAPACK | Single GPU |
| Schur | Complete | Complete | Experimental |
| Reordering | Complete | Complete | Experimental |
| Eigenvectors | Complete | — | — |
Generalized eigenvalue problems:
| Shared memory | Distributed memory | CUDA | |
|---|---|---|---|
| Hessenberg | LAPACK | 3rd party | — |
| Schur | Complete | Complete | Experimental |
| Reordering | Complete | Complete | Experimental |
| Eigenvectors | Complete | — | — |
Authors
StarNEig has been developed at the Department of Computing Science of Umeå University, Sweden. The following people have contributed to the library:
- Angelika Schwarz (standard eigenvectors)
- Bo Kågström (coordinator and scientific director for the NLAFET project, documentation)
- Carl Christian Kjelgaard Mikkelsen (generalized eigenvectors)
- Lars Karlsson (API, documentation)
- Mirko Myllykoski (Hessenberg reduction, Schur reduction, eigenvalue reordering, API, test program, documentation)
Youtube videos
Download and documentation
The stable 0.1-series is recommended for most users:
- Version 0.1 branch ( pdf, html )
- Releases:
- Version 0.1.8 ( pdf, html ) NEW! Prebuild packages for Ubuntu 18.04, 20.04, 21.04 and 21.10.
- Version 0.1.7 ( pdf, html )
- Version 0.1.6 ( pdf, html )
- Version 0.1.5 ( pdf, html )
- Version 0.1.4 ( pdf, html ) NEW! Prebuild packages for Ubuntu 18.04/20.04.
- Version 0.1.3 ( pdf, html ) NEW! Improved Hessenberg reduction.
- Version 0.1.2 ( pdf, html )
- Version 0.1.1 ( pdf, html ) NEW! Major bug fix (stall).
- Version 0.1.0 ( pdf, html )
- Beta releases:
- Version 0.1-beta.6 ( pdf, html )
- Version 0.1-beta.5 ( pdf, html )
- Version 0.1-beta.4 ( pdf, html )
- Version 0.1-beta.3 ( pdf, html )
- Version 0.1-beta.2 ( pdf, html )
- Version 0.1-beta.1 ( pdf, html )
The development series is under continuous development and considered unstable:
- Master branch ( pdf, html )

