 |
StarNEig Library
version v0.1-beta.1
A task-based library for solving nonsymmetric eigenvalue problems
|
 |
StarNEig Library
version v0.1-beta.1
A task-based library for solving nonsymmetric eigenvalue problems
|
StarNEig library aims to provide a full suite of algorithms for solving non-symmetric (generalized) eigenvalue problems. The library is built on top of the StarPU runtime system and targets both shared memory and distributed memory machines. Some components of the library support GPUs.
The four main components of the library are:
The library has been developed as a part of the NLAFET project. The project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 671633. Support has also been received from eSSENCE, a collaborative e-Science programme funded by the Swedish Government via the Swedish Research Council (VR).
The library is currently in a beta state and only real arithmetic is supported. In addition, some interface functions are implemented as LAPACK and ScaLAPACK wrappers.
Current status with standard eigenvalue problems:
| Component | Shared memory | Distributed memory | Accelerators (GPUs) |
|---|---|---|---|
| Hessenberg reduction | Complete | ScaLAPACK wrapper | Single GPU |
| Schur reduction | Complete | Experimental | Experimental |
| Eigenvalue reordering | Complete | Complete | Experimental |
| Eigenvectors | Complete | Waiting integration | Not planned |
Current status with generalized eigenvalue problems:
| Component | Shared memory | Distributed memory | Accelerators (GPUs) |
|---|---|---|---|
| Hessenberg-triangular reduction | LAPACK wrapper / Planned | ScaLAPACK wrapper | Not planned |
| Generalized Schur reduction | Complete | Experimental | Experimental |
| Generalized eigenvalue reordering | Complete | Complete | Experimental |
| Generalized eigenvectors | Complete | Waiting integration | Not planned |
--disable-cuda-memcpy-peer. It is possible that newer version are also effected by this problem.STARPU_LIMIT_CUDA_MEM environmental variable may fix some GPU related memory allocation problems. For example, if the GPU has 6 GB of memory, then setting STARPU_LIMIT_CUDA_MEM=5500 might help.Given a square matrix 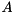 of size
of size 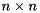 , the standard eigenvalue problem (SEP) consists of finding eigenvalues
, the standard eigenvalue problem (SEP) consists of finding eigenvalues 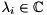 and associated eigenvectors
and associated eigenvectors 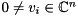 such that
such that
![\[ A v_i = \lambda_i v_i, \text{ for } i = 1, 2, \dots, n. \]](form_22.png)
The eigenvalues are the 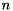 (potentially complex) roots of the polynomial
(potentially complex) roots of the polynomial 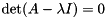 of degree
of degree 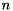 . There is often a full set of
. There is often a full set of 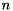 linearly independent eigenvectors, but if there are multiple eigenvalues (i.e., if
linearly independent eigenvectors, but if there are multiple eigenvalues (i.e., if 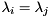 for some
for some 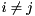 ) then there might not be a full set of independent eigenvectors.
) then there might not be a full set of independent eigenvectors.
The dense matrix 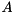 is condensed to Hessenberg form by computing a Hessenberg decomposition
is condensed to Hessenberg form by computing a Hessenberg decomposition
![\[ A = Q_{1} H Q_{1}^{H}, \]](form_26.png)
where 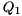 is unitary and
is unitary and 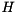 is upper Hessenberg. This is done in order to greatly accelerate the subsequent computation of a Schur decomposition since when working on
is upper Hessenberg. This is done in order to greatly accelerate the subsequent computation of a Schur decomposition since when working on 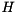 of size
of size 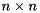 , the amount of work in each iteration of the QR algorithm is reduced from
, the amount of work in each iteration of the QR algorithm is reduced from 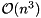 to
to 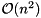 flops.
flops.
Starting from the Hessenberg matrix 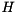 we compute a Schur decomposition
we compute a Schur decomposition
![\[ H = Q_{2} S Q_{2}^H, \]](form_30.png)
where 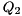 is unitary and
is unitary and 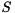 is upper triangular. The eigenvalues of
is upper triangular. The eigenvalues of 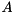 can now be determined as they appear on the diagonal of
can now be determined as they appear on the diagonal of 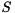 , i.e.,
, i.e., 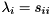 . For real matrices there is a similar decomposition known as the real Schur decomposition
. For real matrices there is a similar decomposition known as the real Schur decomposition
![\[ H = Q_{2} S Q_{2}^T, \]](form_33.png)
where 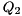 is orthogonal and
is orthogonal and 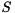 is upper quasi-triangular with
is upper quasi-triangular with 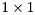 and
and 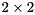 blocks on the diagonal. The
blocks on the diagonal. The 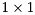 blocks correspond to the real eigenvalues and each
blocks correspond to the real eigenvalues and each 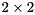 block corresponds to a pair of complex conjugate eigenvalues.
block corresponds to a pair of complex conjugate eigenvalues.
Given a subset consisting of 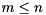 of the eigenvalues, we can reorder the eigenvalues on the diagonal of the Schur form by constructing a unitary matrix
of the eigenvalues, we can reorder the eigenvalues on the diagonal of the Schur form by constructing a unitary matrix 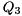 such that
such that
![\[ S = Q_{3} \begin{bmatrix} \hat S_{11} & \hat S_{12} \\ 0 & \hat S_{22} \end{bmatrix} Q_{3}^{H} \]](form_38.png)
and the eigenvalues of the 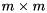 block
block 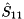 are the selected eigenvalues. The first
are the selected eigenvalues. The first 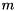 columns of
columns of 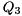 span an invariant subspace associated with the selected eigenvalues.
span an invariant subspace associated with the selected eigenvalues.
Given a subset consisting of 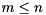 of the eigenvalues
of the eigenvalues 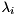 for
for 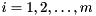 and a Schur decomposition
and a Schur decomposition 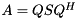 , we can compute for each
, we can compute for each 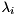 an eigenvector
an eigenvector 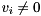 such that
such that 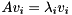 by first computing an eigenvector
by first computing an eigenvector 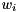 of
of  and then transform it back to the original basis by pre-multiplication with
and then transform it back to the original basis by pre-multiplication with 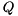 .
.
Given a square matrix pencil 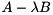 , where
, where 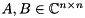 , the generalized eigenvalue problem (GEP) consists of finding generalized eigenvalues
, the generalized eigenvalue problem (GEP) consists of finding generalized eigenvalues 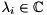 and associated generalized eigenvectors
and associated generalized eigenvectors 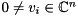 such that
such that
![\[ A v_{i} = \lambda_{i} B v_{i}, \text{ for } i = 1, 2, \dots, n. \]](form_50.png)
The eigenvalues are the 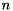 (potentially complex) roots of the polynomial
(potentially complex) roots of the polynomial 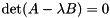 of degree
of degree 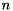 . There is often a full set of
. There is often a full set of 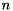 linearly independent generalized eigenvectors, but if there are multiple eigenvalues (i.e., if
linearly independent generalized eigenvectors, but if there are multiple eigenvalues (i.e., if 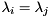 for some
for some 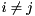 ) then there might not be a full set of independent eigenvectors.
) then there might not be a full set of independent eigenvectors.
At least in principle, a GEP can be transformed into a SEP provided that 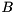 is invertible, since
is invertible, since
![\[ A v = \lambda B v \Leftrightarrow (B^{-1} A) v = \lambda v. \]](form_52.png)
However, in finite precision arithmetic this practice is not recommended.
The dense matrix pair 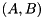 is condensed to Hessenberg-triangular form by computing a Hessenberg-triangular decomposition
is condensed to Hessenberg-triangular form by computing a Hessenberg-triangular decomposition
![\[ A = Q_{1} H Z_{1}^{H}, \quad B = Q_{1} Y Z_{1}^{H}, \]](form_54.png)
where 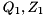 are unitary,
are unitary, 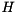 is upper Hessenberg, and
is upper Hessenberg, and 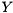 is upper triangular. This is done in order to greatly accelerate the subsequent computation of a generalized Schur decomposition.
is upper triangular. This is done in order to greatly accelerate the subsequent computation of a generalized Schur decomposition.
Starting from the Hessenberg-triangular pencil 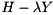 we compute a generalized Schur decomposition
we compute a generalized Schur decomposition
![\[ H = Q_{2} S Z_{2}^H, \quad Y = Q_{2} T Z_{2}^{H}, \]](form_58.png)
where 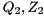 are unitary and
are unitary and 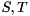 are upper triangular. The eigenvalues of
are upper triangular. The eigenvalues of 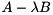 can now be determined from the diagonal element pairs
can now be determined from the diagonal element pairs 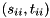 , i.e.,
, i.e., 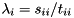 (if
(if 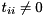 ). If
). If 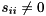 and
and 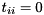 , then
, then 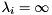 is an infinite eigenvalue of the matrix pair
is an infinite eigenvalue of the matrix pair 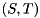 . (If both
. (If both 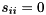 and
and 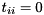 for some
for some 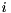 , then the pencil is singular and the eigenvalues are undetermined; all complex numbers are eigenvalues). For real matrix pairs there is a similar decomposition known as the real generalized Schur decomposition
, then the pencil is singular and the eigenvalues are undetermined; all complex numbers are eigenvalues). For real matrix pairs there is a similar decomposition known as the real generalized Schur decomposition
![\[ H = Q_{2} S Z_{2}^T, \quad Y = Q_{2} T Z_{2}^{T}, \]](form_70.png)
where 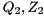 are orthogonal,
are orthogonal, 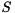 is upper quasi-triangular with
is upper quasi-triangular with 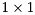 and
and 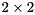 blocks on the diagonal, and
blocks on the diagonal, and 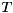 is upper triangular. The
is upper triangular. The 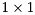 blocks on the diagonal of
blocks on the diagonal of 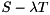 correspond to the real generalized eigenvalues and each
correspond to the real generalized eigenvalues and each 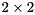 block corresponds to a pair of complex conjugate generalized eigenvalues.
block corresponds to a pair of complex conjugate generalized eigenvalues.
Given a subset consisting of 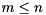 of the generalized eigenvalues, we can reorder the generalized eigenvalues on the diagonal of the generalized Schur form by constructing unitary matrices
of the generalized eigenvalues, we can reorder the generalized eigenvalues on the diagonal of the generalized Schur form by constructing unitary matrices 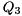 and
and 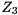 such that
such that
![\[ S - \lambda T = Q_{3} \begin{bmatrix} \hat S_{11} - \lambda \hat T_{11} & \hat S_{12} - \lambda \hat T_{12} \\ 0 & \hat S_{22} - \lambda \hat T_{22} \end{bmatrix} Z_{3}^{H} \]](form_73.png)
and the eigenvalues of the 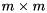 block pencil
block pencil 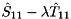 are the selected generalized eigenvalues. The first
are the selected generalized eigenvalues. The first 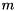 columns of
columns of 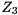 spans a right deflating subspace associated with the selected generalized eigenvalues.
spans a right deflating subspace associated with the selected generalized eigenvalues.
Given a subset consisting of 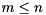 of the eigenvalues
of the eigenvalues 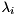 for
for 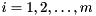 and a generalized Schur decomposition
and a generalized Schur decomposition 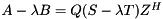 , we can compute for each
, we can compute for each 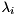 a generalized eigenvector
a generalized eigenvector 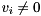 such that
such that 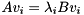 by first computing a generalized eigenvector
by first computing a generalized eigenvector 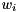 of
of 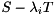 and then transform it back to the original basis by pre-multiplication with
and then transform it back to the original basis by pre-multiplication with 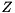 .
.