Functions for solving non-symmetric generalized eigenvalue problems on shared memory systems. More...
Computational functions | |
| starneig_error_t | starneig_GEP_SM_HessenbergTriangular (int n, double A[], int ldA, double B[], int ldB, double Q[], int ldQ, double Z[], int ldZ) |
| Computes a Hessenberg-triangular decomposition of a general matrix pencil. More... | |
| starneig_error_t | starneig_GEP_SM_Schur (int n, double H[], int ldH, double T[], int ldT, double Q[], int ldQ, double Z[], int ldZ, double real[], double imag[], double beta[]) |
| Computes a generalized Schur decomposition given a Hessenberg-triangular decomposition. More... | |
| starneig_error_t | starneig_GEP_SM_ReorderSchur (int n, int selected[], double S[], int ldS, double T[], int ldT, double Q[], int ldQ, double Z[], int ldZ, double real[], double imag[], double beta[]) |
| Reorders selected generalized eigenvalues to the top left corner of a generalized Schur decomposition. More... | |
| starneig_error_t | starneig_GEP_SM_Reduce (int n, double A[], int ldA, double B[], int ldB, double Q[], int ldQ, double Z[], int ldZ, double real[], double imag[], double beta[], int(*predicate)(double real, double imag, double beta, void *arg), void *arg, int selected[], int *num_selected) |
| Computes a (reordered) generalized Schur decomposition given a general matrix pencil. More... | |
| starneig_error_t | starneig_GEP_SM_Eigenvectors (int n, int selected[], double S[], int ldS, double T[], int ldT, double Z[], int ldZ, double X[], int ldX) |
| Computes a generalized eigenvector for each selected generalized eigenvalue. More... | |
Helper functions | |
| starneig_error_t | starneig_GEP_SM_Select (int n, double S[], int ldS, double T[], int ldT, int(*predicate)(double real, double imag, double beta, void *arg), void *arg, int selected[], int *num_selected) |
| Generates a selection array for a Schur-triangular matrix pencil using a user-supplied predicate function. More... | |
Expert computational functions | |
| starneig_error_t | starneig_GEP_SM_Schur_expert (struct starneig_schur_conf *conf, int n, double H[], int ldH, double T[], int ldT, double Q[], int ldQ, double Z[], int ldZ, double real[], double imag[], double beta[]) |
| Computes a generalized Schur decomposition given a Hessenberg-triangular decomposition. More... | |
| starneig_error_t | starneig_GEP_SM_ReorderSchur_expert (struct starneig_reorder_conf *conf, int n, int selected[], double S[], int ldS, double T[], int ldT, double Q[], int ldQ, double Z[], int ldZ, double real[], double imag[], double beta[]) |
| Reorders selected eigenvalues to the top left corner of a generalized Schur decomposition. More... | |
| starneig_error_t | starneig_GEP_SM_Eigenvectors_expert (struct starneig_eigenvectors_conf *conf, int n, int selected[], double S[], int ldS, double T[], int ldT, double Z[], int ldZ, double X[], int ldX) |
| Computes a generalized eigenvector for each selected generalized eigenvalue. More... | |
Detailed Description
Functions for solving non-symmetric generalized eigenvalue problems on shared memory systems.
Function Documentation
◆ starneig_GEP_SM_HessenbergTriangular()
| starneig_error_t starneig_GEP_SM_HessenbergTriangular | ( | int | n, |
| double | A[], | ||
| int | ldA, | ||
| double | B[], | ||
| int | ldB, | ||
| double | Q[], | ||
| int | ldQ, | ||
| double | Z[], | ||
| int | ldZ | ||
| ) |
Computes a Hessenberg-triangular decomposition of a general matrix pencil.
- Remarks
- This function is a wrapper for several LAPACK subroutines.
- Parameters
-
[in] n The order of 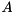 ,
, 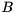 ,
, 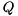 and
and  .
.[in,out] A On entry, the general matrix 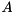 . On exit, the upper Hessenberg matrix
. On exit, the upper Hessenberg matrix 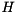 .
.[in] ldA The leading dimension of 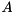 .
.[in,out] B On entry, the general matrix 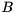 . On exit, the upper triangular matrix
. On exit, the upper triangular matrix  .
.[in] ldB The leading dimension of 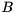 .
.[in,out] Q On entry, the orthogonal matrix 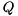 . On exit, the product matrix
. On exit, the product matrix 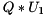 .
.[in] ldQ The leading dimension of 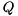 .
.[in,out] Z On entry, the orthogonal matrix  . On exit, the product matrix
. On exit, the product matrix 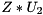 .
.[in] ldZ The leading dimension of  .
.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise.
- Examples:
- gep_sm_full_chain.c.
◆ starneig_GEP_SM_Schur()
| starneig_error_t starneig_GEP_SM_Schur | ( | int | n, |
| double | H[], | ||
| int | ldH, | ||
| double | T[], | ||
| int | ldT, | ||
| double | Q[], | ||
| int | ldQ, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | real[], | ||
| double | imag[], | ||
| double | beta[] | ||
| ) |
Computes a generalized Schur decomposition given a Hessenberg-triangular decomposition.
- Parameters
-
[in] n The order of 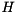 ,
,  ,
, 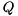 and
and  .
.[in,out] H On entry, the upper Hessenberg matrix 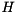 . On exit, the Schur matrix
. On exit, the Schur matrix  .
.[in] ldH The leading dimension of 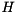 .
.[in,out] T On entry, the upper triangular matrix  . On exit, the upper triangular matrix
. On exit, the upper triangular matrix 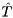 .
.[in] ldT The leading dimension of  .
.[in,out] Q On entry, the orthogonal matrix 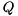 . On exit, the product matrix
. On exit, the product matrix 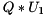 .
.[in] ldQ The leading dimension of 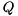 .
.[in,out] Z On entry, the orthogonal matrix  . On exit, the product matrix
. On exit, the product matrix 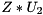 .
.[in] ldZ The leading dimension of  .
.[out] real An array of the same size as 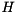 containing the real parts of the
containing the real parts of the 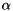 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] imag An array of the same size as 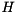 containing the imaginary parts of the
containing the imaginary parts of the 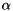 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] beta An array of the same size as 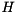 containing the
containing the 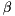 values of computed generalized eigenvalues.
values of computed generalized eigenvalues.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise. STARNEIG_DID_NOT_CONVERGE if the QZ algorithm failed to converge.
- Examples:
- gep_sm_full_chain.c.
◆ starneig_GEP_SM_ReorderSchur()
| starneig_error_t starneig_GEP_SM_ReorderSchur | ( | int | n, |
| int | selected[], | ||
| double | S[], | ||
| int | ldS, | ||
| double | T[], | ||
| int | ldT, | ||
| double | Q[], | ||
| int | ldQ, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | real[], | ||
| double | imag[], | ||
| double | beta[] | ||
| ) |
Reorders selected generalized eigenvalues to the top left corner of a generalized Schur decomposition.
- Parameters
-
[in] n The order of 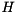 ,
,  ,
, 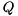 and
and  .
.[in,out] selected The selection array. On entry, the initial positions of the selected generalized eigenvalues. On exit, the final positions of all correctly placed selected generalized eigenvalues. In case of failure, the number of 1's in the output may be less than the number of 1's in the input. [in,out] S On entry, the Schur matrix  . On exit, the updated Schur matrix
. On exit, the updated Schur matrix 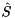 .
.[in] ldS The leading dimension of  .
.[in,out] T On entry, the upper triangular  . On exit, the updates upper triangular matrix
. On exit, the updates upper triangular matrix 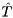 .
.[in] ldT The leading dimension of  .
.[in,out] Q On entry, the orthogonal matrix 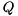 . On exit, the product matrix
. On exit, the product matrix 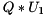 .
.[in] ldQ The leading dimension of 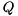 .
.[in,out] Z On entry, the orthogonal matrix  . On exit, the product matrix
. On exit, the product matrix 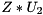 .
.[in] ldZ The leading dimension of  .
.[out] real An array of the same size as  containing the real parts of the
containing the real parts of the 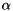 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] imag An array of the same size as  containing the imaginary parts of the
containing the imaginary parts of the 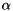 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] beta An array of the same size as  containing the
containing the 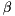 values of computed generalized eigenvalues.
values of computed generalized eigenvalues.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise. STARNEIG_PARTIAL_REORDERING if the generalized Schur form is not fully reordered.
- See also
- starneig_GEP_SM_Select
- Examples:
- gep_sm_full_chain.c.
◆ starneig_GEP_SM_Reduce()
| starneig_error_t starneig_GEP_SM_Reduce | ( | int | n, |
| double | A[], | ||
| int | ldA, | ||
| double | B[], | ||
| int | ldB, | ||
| double | Q[], | ||
| int | ldQ, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | real[], | ||
| double | imag[], | ||
| double | beta[], | ||
| int(*)(double real, double imag, double beta, void *arg) | predicate, | ||
| void * | arg, | ||
| int | selected[], | ||
| int * | num_selected | ||
| ) |
Computes a (reordered) generalized Schur decomposition given a general matrix pencil.
- Parameters
-
[in] n The order of 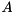 ,
, 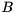 ,
, 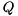 and
and  .
.[in,out] A On entry, the general matrix 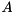 . On exit, the Schur matrix
. On exit, the Schur matrix  .
.[in] ldA The leading dimension of 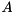 .
.[in,out] B On entry, the general matrix 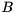 . On exit, the upper triangular matrix
. On exit, the upper triangular matrix  .
.[in] ldB The leading dimension of 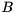 .
.[in,out] Q On entry, the orthogonal matrix 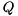 . On exit, the product matrix
. On exit, the product matrix 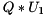 .
.[in] ldQ The leading dimension of 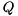 .
.[in,out] Z On entry, the orthogonal matrix  . On exit, the product matrix
. On exit, the product matrix 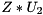 .
.[in] ldZ The leading dimension of  .
.[out] real An array of the same size as 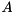 containing the real parts of the
containing the real parts of the 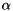 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] imag An array of the same size as 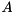 containing the imaginary parts of the
containing the imaginary parts of the 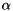 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] beta An array of the same size as 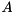 containing the
containing the 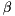 values of computed generalized eigenvalues.
values of computed generalized eigenvalues.[in] predicate A function that takes a (complex) generalized eigenvalue as input and returns non-zero if it should be selected. For complex conjugate pairs of generalized eigenvalues, the predicate is called only for the generalized eigenvalue with positive imaginary part and the corresponding 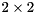 block is either selected or deselected. The reordering step is skipped if the argument is a NULL pointer.
block is either selected or deselected. The reordering step is skipped if the argument is a NULL pointer.[in] arg An optional argument for the predicate function. [out] selected The final positions of all correctly placed selected generalized eigenvalues. [out] num_selected The number of selected generalized eigenvalues (a complex conjugate pair is counted as two selected generalized eigenvalues).
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise. STARNEIG_DID_NOT_CONVERGE if the QZ algorithm failed to converge. STARNEIG_PARTIAL_REORDERING if the generalized Schur form is not fully reordered.
- Examples:
- gep_sm_eigenvectors.c.
◆ starneig_GEP_SM_Eigenvectors()
| starneig_error_t starneig_GEP_SM_Eigenvectors | ( | int | n, |
| int | selected[], | ||
| double | S[], | ||
| int | ldS, | ||
| double | T[], | ||
| int | ldT, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | X[], | ||
| int | ldX | ||
| ) |
Computes a generalized eigenvector for each selected generalized eigenvalue.
- Parameters
-
[in] n The order of  and
and 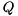 and the number of rows of
and the number of rows of 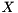 .
.[in] selected The selection array specifying the locations of the selected generalized eigenvalues. The number of 1's in the array is the same as the number of columns in 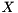 .
.[in] S The Schur matrix  .
.[in] ldS The leading dimension of  .
.[in] T The upper triangular matrix  .
.[in] ldT The leading dimension of  .
.[in] Z The orthogonal matrix  .
.[in] ldZ The leading dimension of  .
.[out] X A matrix with 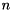 rows and one column for each selected generalized eigenvalue. The columns represent the computed generalized eigenvectors as previously described.
rows and one column for each selected generalized eigenvalue. The columns represent the computed generalized eigenvectors as previously described.[in] ldX The leading dimension of 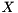 .
.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise.
- See also
- starneig_GEP_SM_Select
- Examples:
- gep_sm_eigenvectors.c.
◆ starneig_GEP_SM_Select()
| starneig_error_t starneig_GEP_SM_Select | ( | int | n, |
| double | S[], | ||
| int | ldS, | ||
| double | T[], | ||
| int | ldT, | ||
| int(*)(double real, double imag, double beta, void *arg) | predicate, | ||
| void * | arg, | ||
| int | selected[], | ||
| int * | num_selected | ||
| ) |
Generates a selection array for a Schur-triangular matrix pencil using a user-supplied predicate function.
- Parameters
-
[in] n The order of  and
and  .
.[in] S The Schur matrix  .
.[in] ldS The leading dimension of  .
.[in] T The upper triangular matrix  .
.[in] ldT The leading dimension of  .
.[in] predicate A function that takes a (complex) generalized eigenvalue as input and returns non-zero if it should be selected. For complex conjugate pairs of generalized eigenvalues, the predicate is called only for the generallized eigenvalue with positive imaginary part and the corresponding 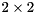 block is either selected or deselected.
block is either selected or deselected.[in] arg An optional argument for the predicate function. [out] selected The selection array. Both elements of a selected complex conjugate pair are set to 1. [out] num_selected The number of selected generalized eigenvalues (a complex conjugate pair is counted as two selected generalized eigenvalues).
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise.
- Examples:
- gep_sm_eigenvectors.c, and gep_sm_full_chain.c.
◆ starneig_GEP_SM_Schur_expert()
| starneig_error_t starneig_GEP_SM_Schur_expert | ( | struct starneig_schur_conf * | conf, |
| int | n, | ||
| double | H[], | ||
| int | ldH, | ||
| double | T[], | ||
| int | ldT, | ||
| double | Q[], | ||
| int | ldQ, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | real[], | ||
| double | imag[], | ||
| double | beta[] | ||
| ) |
Computes a generalized Schur decomposition given a Hessenberg-triangular decomposition.
- Parameters
-
[in] conf Configuration structure. [in] n The order of 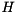 ,
,  ,
, 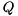 and
and  .
.[in,out] H On entry, the upper Hessenberg matrix 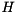 . On exit, the Schur matrix
. On exit, the Schur matrix  .
.[in] ldH The leading dimension of 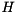 .
.[in,out] T On entry, the upper triangular matrix  . On exit, the upper triangular matrix
. On exit, the upper triangular matrix 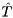 .
.[in] ldT The leading dimension of  .
.[in,out] Q On entry, the orthogonal matrix 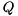 . On exit, the product matrix
. On exit, the product matrix 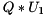 .
.[in] ldQ The leading dimension of 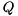 .
.[in,out] Z On entry, the orthogonal matrix  . On exit, the product matrix
. On exit, the product matrix 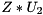 .
.[in] ldZ The leading dimension of  .
.[out] real An array of the same size as 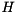 containing the real parts of the
containing the real parts of the 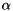 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] imag An array of the same size as 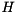 containing the imaginary parts of the
containing the imaginary parts of the 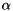 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] beta An array of the same size as 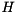 containing the
containing the 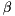 values of computed generalized eigenvalues.
values of computed generalized eigenvalues.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise.
◆ starneig_GEP_SM_ReorderSchur_expert()
| starneig_error_t starneig_GEP_SM_ReorderSchur_expert | ( | struct starneig_reorder_conf * | conf, |
| int | n, | ||
| int | selected[], | ||
| double | S[], | ||
| int | ldS, | ||
| double | T[], | ||
| int | ldT, | ||
| double | Q[], | ||
| int | ldQ, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | real[], | ||
| double | imag[], | ||
| double | beta[] | ||
| ) |
Reorders selected eigenvalues to the top left corner of a generalized Schur decomposition.
- Parameters
-
[in] conf Configuration structure. [in] n The order of 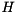 ,
,  ,
, 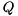 and
and  .
.[in,out] selected The selection array. [in,out] S On entry, the Schur matrix  . On exit, the updated Schur matrix
. On exit, the updated Schur matrix 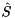 .
.[in] ldS The leading dimension of  .
.[in,out] T On entry, the upper triangular  . On exit, the updates upper triangular matrix
. On exit, the updates upper triangular matrix 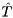 .
.[in] ldT The leading dimension of  .
.[in,out] Q On entry, the orthogonal matrix 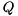 . On exit, the product matrix
. On exit, the product matrix 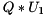 .
.[in] ldQ The leading dimension of 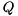 .
.[in,out] Z On entry, the orthogonal matrix  . On exit, the product matrix
. On exit, the product matrix 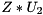 .
.[in] ldZ The leading dimension of  .
.[out] real An array of the same size as  containing the real parts of the
containing the real parts of the 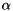 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] imag An array of the same size as  containing the imaginary parts of the
containing the imaginary parts of the 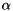 values of the computed generalized eigenvalues.
values of the computed generalized eigenvalues.[out] beta An array of the same size as  containing the
containing the 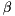 values of computed generalized eigenvalues.
values of computed generalized eigenvalues.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise.
◆ starneig_GEP_SM_Eigenvectors_expert()
| starneig_error_t starneig_GEP_SM_Eigenvectors_expert | ( | struct starneig_eigenvectors_conf * | conf, |
| int | n, | ||
| int | selected[], | ||
| double | S[], | ||
| int | ldS, | ||
| double | T[], | ||
| int | ldT, | ||
| double | Z[], | ||
| int | ldZ, | ||
| double | X[], | ||
| int | ldX | ||
| ) |
Computes a generalized eigenvector for each selected generalized eigenvalue.
- Parameters
-
[in] conf Configuration structure. [in] n The order of  and
and 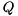 and the number of rows of
and the number of rows of 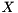 .
.[in] selected The selection array specifying the locations of the selected generalized eigenvalues. The number of 1's in the array is the same as the number of columns in 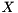 .
.[in] S The Schur matrix  .
.[in] ldS The leading dimension of  .
.[in] T The upper triangular matrix  .
.[in] ldT The leading dimension of  .
.[in] Z The orthogonal matrix  .
.[in] ldZ The leading dimension of  .
.[out] X A matrix with 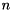 rows and one column for each selected generalized eigenvalue. The columns represent the computed generalized eigenvectors as previously described.
rows and one column for each selected generalized eigenvalue. The columns represent the computed generalized eigenvectors as previously described.[in] ldX The leading dimension of 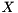 .
.
- Returns
- STARNEIG_SUCCESS (0) on success. Negative integer -i when i'th argument is invalid. Positive error code otherwise.
- See also
- starneig_GEP_SM_Select
