 |
StarNEig Library
version v0.1-beta.1
A task-based library for solving nonsymmetric eigenvalue problems
|
 |
StarNEig Library
version v0.1-beta.1
A task-based library for solving nonsymmetric eigenvalue problems
|
The library provides 12 interface functions for the generalized case:
Given a general matrix 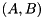 , the starneig_GEP_SM_HessenbergTriangular() and starneig_GEP_DM_HessenbergTriangular() interface functions compute a Hessenberg-triangular decomposition
, the starneig_GEP_SM_HessenbergTriangular() and starneig_GEP_DM_HessenbergTriangular() interface functions compute a Hessenberg-triangular decomposition
![\[ (A,B) = U_1 * (H,T) * U_2^T, \]](form_89.png)
where 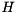 is upper Hessenberg,
is upper Hessenberg, 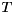 is upper triangular, and
is upper triangular, and 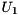 and
and 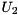 are orthogonal. On exit,
are orthogonal. On exit, 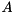 is overwritten by
is overwritten by 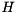 ,
, 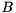 is overwritten by
is overwritten by 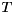 , and
, and 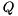 and
and 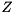 (which are orthogonal matrices on entry) are overwritten by
(which are orthogonal matrices on entry) are overwritten by
![\[ Q \gets Q * U_1 \text{ and } Z \gets Z * U_2. \]](form_92.png)
Given a Hessenberg-triangular decomposition
![\[ (A,B) = Q * (H,T) * Z^T \]](form_93.png)
of a general matrix pencil 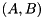 , the starneig_GEP_SM_Schur() and starneig_GEP_DM_Schur() interface functions function compute a generalized Schur decomposition
, the starneig_GEP_SM_Schur() and starneig_GEP_DM_Schur() interface functions function compute a generalized Schur decomposition
![\[ (A,B) = Q * ( U_1 * (S,\hat{T}) * U_2^T ) * Z^T, \]](form_94.png)
where 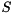 is upper quasi-triangular with
is upper quasi-triangular with 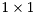 and
and 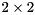 blocks on the diagonal,
blocks on the diagonal, 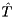 is a upper triangular matrix, and
is a upper triangular matrix, and 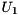 and
and 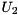 are orthogonal.
are orthogonal.
On exit, 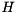 is overwritten by
is overwritten by 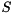 ,
, 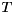 is overwritten by
is overwritten by 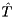 , and
, and 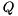 and
and 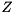 are overwritten by
are overwritten by
![\[ Q \gets Q * U_1 \text{ and } Z \gets Z * U_2. \]](form_92.png)
The computed generalized eigenvalues are returned as a pair of values 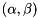 such that
such that 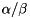 gives the actual generalized eigenvalue. The quantity
gives the actual generalized eigenvalue. The quantity 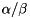 may overflow.
may overflow.
Given a generalized Schur decomposition
![\[ (A,B) = Q * (S,T) * Z^T \]](form_97.png)
of a general matrix pencil 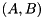 and a selection of generalized eigenvalues, the starneig_GEP_SM_ReorderSchur() and starneig_GEP_DM_ReorderSchur() interface functions attempt to reorder the selected generalized eigenvalues to the top left corner of an updated generalized Schur decomposition by an orthogonal similarity transformation
and a selection of generalized eigenvalues, the starneig_GEP_SM_ReorderSchur() and starneig_GEP_DM_ReorderSchur() interface functions attempt to reorder the selected generalized eigenvalues to the top left corner of an updated generalized Schur decomposition by an orthogonal similarity transformation
![\[ (A,B) = Q * ( U_1 * (\hat{S},\hat{T}) * U_2^T ) * Z^T. \]](form_98.png)
On exit, 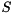 is overwritten by
is overwritten by 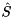 ,
, 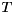 is overwritten by
is overwritten by 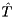 , and
, and 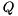 and
and 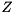 are overwritten by
are overwritten by
![\[ Q \gets Q * U_1 \text{ and } Z \gets Z * U_2. \]](form_92.png)
Reordering may in rare cases fail. In such cases the output is guaranteed to be a Schur decomposition and all (if any) selected generalized eigenvalues that are correctly placed are marked in the selection array on exit.
Reordering may perturb the generalized eigenvalues and the generalized eigenvalues after reordering are returned. The computed generalized eigenvalues are returned as a pair of values 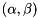 such that
such that 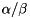 gives the actual generalized eigenvalue. The quantity
gives the actual generalized eigenvalue. The quantity 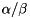 may overflow.
may overflow.
Given a general matrix pencil 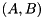 , the starneig_GEP_SM_Reduce() and starneig_GEP_DM_Reduce() interface functions compute a (reordered) generalized Schur decomposition
, the starneig_GEP_SM_Reduce() and starneig_GEP_DM_Reduce() interface functions compute a (reordered) generalized Schur decomposition
![\[ (A,B) = U_1 * (S,T) * U_2^T, \]](form_99.png)
where 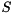 is upper quasi-triangular with
is upper quasi-triangular with  and
and 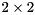 blocks on the diagonal,
blocks on the diagonal, 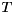 is a upper triangular matrix, and
is a upper triangular matrix, and 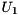 and
and 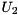 are orthogonal. Optionally, the interface functions attempt to reorder selected generalized eigenvalues to the top left corner of the generalized Schur decomposition.
are orthogonal. Optionally, the interface functions attempt to reorder selected generalized eigenvalues to the top left corner of the generalized Schur decomposition.
On exit, 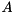 is overwritten by
is overwritten by 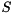 ,
, 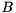 is overwritten by
is overwritten by 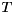 , and
, and 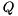 and
and 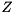 (which are orthogonal matrices on entry) are overwritten by
(which are orthogonal matrices on entry) are overwritten by
![\[ Q \gets Q * U_1 \text{ and } Z \gets Z * U_2. \]](form_92.png)
The computed generalized eigenvalues are returned as a pair of values 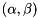 such that
such that 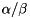 gives the actual generalized eigenvalue. The quantity
gives the actual generalized eigenvalue. The quantity 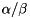 may overflow.
may overflow.
Reordering may in rare cases fail. In such cases the output is guaranteed to be a Schur-triangular decomposition and all (if any) selected generalized eigenvalues that are correctly placed are marked in the selection array on exit.
Given a generalized Schur decomposition
![\[ (A,B) = Q * (S,T) * Z^T \]](form_97.png)
of a general matrix pencil 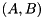 and a selection of generalized eigenvalues, the starneig_GEP_SM_Eigenvectors() and starneig_GEP_DM_Eigenvectors() interface functions compute and return a generalized eigenvector for each of the selected generalized eigenvalues.
and a selection of generalized eigenvalues, the starneig_GEP_SM_Eigenvectors() and starneig_GEP_DM_Eigenvectors() interface functions compute and return a generalized eigenvector for each of the selected generalized eigenvalues.
The generalized eigenvectors are stored as columns in the output matrix 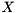 in the same order as their corresponding generalized eigenvalues appear in the selection array. A real generalized eigenvector is stored as a single column. The real and imaginary parts of a complex generalized eigenvector are stored as consecutive columns.
in the same order as their corresponding generalized eigenvalues appear in the selection array. A real generalized eigenvector is stored as a single column. The real and imaginary parts of a complex generalized eigenvector are stored as consecutive columns.
For a selected pair of complex conjugate generalized eigenvalues, a generalized eigenvector is computed only for the generalized eigenvalue with positive imaginary part. Thus, every selected generalized eigenvalue contributes one column to the output matrix and thus the number of selected generalized eigenvalues is equal to the number of columns of 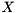 .
.
Given a Schur-triangular matrix pencil 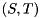 and a predicate function, the starneig_GEP_SM_Select() and starneig_GEP_DM_Select() interface functions conveniently generate a correct selection array and count the number of selected generalized eigenvalues. The count is useful when allocating storage for the generalized eigenvector matrix computed by starneig_GEP_DM_Eigenvectors().
and a predicate function, the starneig_GEP_SM_Select() and starneig_GEP_DM_Select() interface functions conveniently generate a correct selection array and count the number of selected generalized eigenvalues. The count is useful when allocating storage for the generalized eigenvector matrix computed by starneig_GEP_DM_Eigenvectors().
See modules Shared Memory / Generalized EVP and Distributed Memory / Generalized EVP for further information. See also examples gep_sm_full_chain.c, gep_dm_full_chain.c and gep_sm_eigenvectors.c.