 |
StarNEig Library
version v0.1-beta.1
A task-based library for solving nonsymmetric eigenvalue problems
|
 |
StarNEig Library
version v0.1-beta.1
A task-based library for solving nonsymmetric eigenvalue problems
|
The library provides 12 interface functions for the standard case:
Given a general matrix 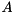 , the starneig_SEP_SM_Hessenberg() and starneig_SEP_DM_Hessenberg() interface functions compute a Hessenberg decomposition
, the starneig_SEP_SM_Hessenberg() and starneig_SEP_DM_Hessenberg() interface functions compute a Hessenberg decomposition
![\[ A = U * H * U^T, \]](form_80.png)
where 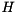 is upper Hessenberg and
is upper Hessenberg and 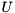 is orthogonal. On exit,
is orthogonal. On exit, 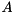 is overwritten by
is overwritten by 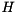 and
and 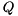 (which is an orthogonal matrix on entry) is overwritten by
(which is an orthogonal matrix on entry) is overwritten by
![\[ Q \gets Q * U. \]](form_82.png)
Given a Hessenberg decomposition
![\[ A = Q * H * Q^T, \]](form_83.png)
of a general matrix 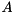 , the starneig_SEP_SM_Schur() and starneig_SEP_DM_Schur() interface functions compute a Schur decomposition
, the starneig_SEP_SM_Schur() and starneig_SEP_DM_Schur() interface functions compute a Schur decomposition
![\[ A = Q * ( U * S * U^T ) * Q^T \]](form_84.png)
where 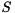 is upper quasi-triangular with
is upper quasi-triangular with 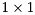 and
and 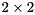 blocks on the diagonal (Schur matrix) and
blocks on the diagonal (Schur matrix) and 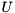 is orthogonal. On exit,
is orthogonal. On exit, 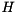 is overwritten by
is overwritten by 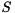 and
and 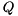 is overwritten by
is overwritten by
![\[ Q \gets Q * U. \]](form_82.png)
Given a Schur decomposition
![\[ A = Q * S * Q^T \]](form_85.png)
of a general matrix 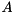 and a selection of eigenvalues, the starneig_SEP_SM_ReorderSchur() and starneig_SEP_DM_ReorderSchur() interface functions attempt to reorder the selected eigenvalues to the top left corner of an updated Schur matrix
and a selection of eigenvalues, the starneig_SEP_SM_ReorderSchur() and starneig_SEP_DM_ReorderSchur() interface functions attempt to reorder the selected eigenvalues to the top left corner of an updated Schur matrix 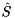 by an orthogonal similarity transformation
by an orthogonal similarity transformation
![\[ A = Q * ( U * \hat{S} * U^T ) * Q^T. \]](form_86.png)
On exit, 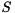 is overwritten by
is overwritten by 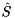 and
and 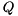 is overwritten by
is overwritten by
![\[ Q \gets Q * U. \]](form_82.png)
Reordering may in rare cases fail. In such cases the output is guaranteed to be a Schur decomposition and all (if any) selected eigenvalues that are correctly placed are marked in the selection array on exit. Reordering may perturb the eigenvalues and the eigenvalues after reordering are returned.
Given a general matrix 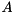 , the starneig_SEP_SM_Reduce() and starneig_SEP_DM_Reduce() interface functions compute a (reordered) Schur decomposition
, the starneig_SEP_SM_Reduce() and starneig_SEP_DM_Reduce() interface functions compute a (reordered) Schur decomposition
![\[ A = U * S * U^T, \]](form_87.png)
where 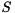 is upper quasi-triangular with
is upper quasi-triangular with 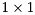 and
and 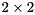 blocks on the diagonal (Schur matrix) and
blocks on the diagonal (Schur matrix) and 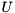 is orthogonal. Optionally, the interface functions attempt to reorder selected eigenvalues to the top left corner of the Schur matrix
is orthogonal. Optionally, the interface functions attempt to reorder selected eigenvalues to the top left corner of the Schur matrix 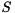 .
.
On exit, 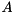 is overwritten by
is overwritten by 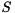 and
and 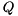 (which is an orthogonal matrix on entry) is overwritten by
(which is an orthogonal matrix on entry) is overwritten by
![\[ Q \gets Q * U. \]](form_82.png)
Reordering may in rare cases fail. In such cases the output is guaranteed to be a Schur decomposition and all (if any) selected eigenvalues that are correctly placed are marked in the selection array on exit. Reordering may perturb the eigenvalues and the eigenvalues after reordering are returned.
Given a Schur decomposition
![\[ A = Q * S * Q^T \]](form_85.png)
of a general matrix 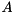 and a selection of eigenvalues, the starneig_SEP_SM_Eigenvectors() and starneig_SEP_DM_Eigenvectors() interface functions compute and return an eigenvector for each of the selected eigenvalues.
and a selection of eigenvalues, the starneig_SEP_SM_Eigenvectors() and starneig_SEP_DM_Eigenvectors() interface functions compute and return an eigenvector for each of the selected eigenvalues.
The eigenvectors are stored as columns in the output matrix 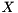 in the same order as their corresponding eigenvalues appear in the selection array. A real eigenvector is stored as a single column. The real and imaginary parts of a complex eigenvector are stored as consecutive columns.
in the same order as their corresponding eigenvalues appear in the selection array. A real eigenvector is stored as a single column. The real and imaginary parts of a complex eigenvector are stored as consecutive columns.
For a selected pair of complex conjugate eigenvalues, an eigenvector is computed only for the eigenvalue with positive imaginary part. Thus, every selected eigenvalue contributes one column to the output matrix and thus the number of selected eigenvalues is equal to the number of columns of 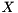 .
.
Given a Schur matrix and a predicate function, the starneig_SEP_SM_Select() and starneig_SEP_DM_Select() interface functions conveniently generate a correct selection array and count the number of selected eigenvalues. The count is useful when allocating storage for the eigenvector matrix computed by the starneig_SEP_SM_Eigenvectors() and starneig_SEP_DM_Eigenvectors() interface functions.
See modules Shared Memory / Standard EVP and Distributed Memory / Standard EVP for further information. See also examples sep_sm_full_chain.c, sep_dm_full_chain.c and sep_sm_eigenvectors.c.