The STARNEIG_HINT_DM initialization flag tells the library to configure itself for distributed memory computation. The flag is indented to be only a hint and the library will automatically reconfigure itself for the correct computation mode. A user is allowed to mix shared memory and distributed memory functions without reninitializing the library. The library is intended to be run in a hybrid configuration (each MPI rank is mapped to several CPU cores). Failing to do so leads to CPU core oversubscription. It is generally a good idea to map each MPI rank to a full node or a NUMA island / CPU socket:

# OpenMPI / one rank per node:
$ mpirun -n RANKS --map-by ppr:1:node --bind-to none ...
# OpenMPI / one rank per socket:
$ mpirun -n RANKS --map-by ppr:1:socket --bind-to socket ...
# Intel MPI / one rank per node:
$ mpirun -n RANKS -binding "pin=on;domain=node" ...
# Intel MPI / one rank per socket:
$ mpirun -n RANKS -binding "pin=on;domain=socket" ...

Attention: StarPU attempts to bind the worker threads to the available CPU cores. This may sometimes conflict with the MPI library and/or the batch system CPU core allocation. StarNEig library attempts to correct for by factoring in the CPU core binding mask. However, if neither the MPI library nor the batch system enforces such a binding mask, it is possible that several StarPU worker threads end up bound to a same CPU core. In such a situation, it is recommended that a user disables the StarPU thread binding explicitly:
STARPU_WORKERS_NOBIND=1 mpirun ...
This is particularly important when several ranks / processes are mapped to a same node.

The library assumes that the MPI library is already initialized when the starneig_node_init() interface function is called with the STARNEIG_HINT_DM flag or when the library reconfigures itself for distributed memory after a user has called a distributed memory interface function. The MPI library should be initialized either in the serialized mode:

int thread_support;
MPI_Init_thread(
    &argc, (char ***)&argv, MPI_THREAD_SERIALIZED, &thread_support);
if (thread_support < MPI_THREAD_SERIALIZED) {
    fprintf(stderr,
        "MPI_THREAD_SERIALIZED is not supported. Aborting...\n");
    abort();
}

Or in the multi-threaded mode:

int thread_support;
MPI_Init_thread(
    &argc, (char ***)&argv, MPI_THREAD_MULTIPLE, &thread_support);
if (thread_support < MPI_THREAD_SERIALIZED) {
    fprintf(stderr,
        "MPI_THREAD_SERIALIZED is not supported. Aborting...\n");
    abort();
} else if (thread_support < MPI_THREAD_MULTIPLE) {
    fprintf(stderr,
        "Warning: MPI_THREAD_MULTIPLE is not supported.\n");
}

A user is allowed to change the library MPI communicator with the starneig_mpi_set_comm() interface function. This interface function should be called before the library is initialized.

Data distribution

Distributed matrices are represented using two opaque objects:

Data distribution (starneig_distr_t)
Distributed matrix (starneig_distr_matrix_t)

Each matrix is divided into rectangular blocks of uniform size (excluding the last block row and column):

A matrix divided into rectangular blocks of uniform size.

The blocks are indexed using a two-dimensional index space. A data distribution encapsulates an arbitrary mapping from this two-dimensional block index space to the one-dimensional MPI rank space:

An example of a block mapping.

In the above example, the rank 0 owns the blocks (0,1), (1,2), (1,5), (1,6), (2,6), (3,0) and (3,5). Naturally, a data distribution can describe a two-dimensional block cyclic distribution that is very common with ScaLAPACK subroutines:

An example of a row-major ordered two-dimensional block cyclic mapping.

A data distribution can be created using one of the following interface functions:

starneig_distr_init() creates a default distribution (row-major ordered two-dimensional block cyclic distribution with a squarish mesh).
starneig_distr_init_mesh() creates a row-major or column-major ordered two-dimensional block cyclic distribution with desired number of rows and columns in the mesh.
starneig_distr_init_func() creates an arbitrary distribution defined by a function.

Fox example,

starneig_distr_t distr = starneig_distr_init_mesh(4, 6, STARNEIG_ORDER_DEFAULT);

would create a two-dimensional block cyclic distribution with 4 rows and 6 columns in the mesh. Alternatively, a user can create an equivalent data distribution using the starneig_distr_init_func() interface function:

// additional distribution function argument structure
struct block_cyclic_arg {
    int rows;   // the number of rows in the process mesh
    int cols;   // the number of columns in the process mesh
};
// distribution function (row-major ordered 2D block cyclic distribution)
int block_cyclic_func(int i, int j, void *arg)
{
    struct block_cyclic_arg *mesh = (struct block_cyclic_arg *) arg;
    return (i % mesh->rows) * mesh->cols + j % mesh->cols;
}
void func(...)
{
    ...
    struct block_cyclic_arg arg = { .rows = 4, .cols = 6 };
    starneig_distr_t distr =
        starneig_distr_init_func(&block_cyclic_func, &arg, sizeof(arg));
    ...
}

A data distribution is destroyed with the starneig_distr_destroy() interface function.

Remarks: Certain interface functions (starneig_SEP_DM_Hessenberg(), starneig_SEP_DM_Reduce(), starneig_GEP_DM_HessenbergTriangular(), and starneig_GEP_DM_Reduce()) are wrappers for / use several ScaLAPACK subroutines. The involved matrices should thus have a two-dimensional block cyclic data distribution. The library will automatically convert the matrices to a compatible format but this requires extra memory.

Distributed matrix

A distributed matrix is created using the starneig_distr_matrix_create() interface function. The function call will automatically allocate the required local resources. For example,

starneig_distr_t distr =
    starneig_distr_init_mesh(4, 6, STARNEIG_ORDER_DEFAULT);
starneig_distr_matrix_t dA =
    starneig_distr_matrix_create(m, n, bm, bn, STARNEIG_REAL_DOUBLE, distr);

would create a 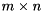$m \times n$ double-precision real matrix that is distributed in a two-dimensional block cyclic fashion in 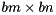$bm \times bn$ blocks. Or,

starneig_distr_matrix_t dB =

starneig_distr_matrix_create(n, n, -1, -1, STARNEIG_REAL_DOUBLE, NULL);

would create a 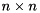$n \times n$ double-precision real matrix with a default data distribution (NULL argument) and a default block size (-1, -1).

Attention: StarNEig library is designed to use much larger distributed blocks than ScaLAPACK. Selecting a too small distributed block size will be detrimental to the performance.

A user may access the locally owned blocks using the starneig_distr_matrix_get_blocks() interface function. A distributed matrix is destroyed using the starneig_distr_matrix_destroy() interface function. This will deallocate all local resources. See module Distributed Memory / Distributed matrices for further information.

Remarks: Certain interface functions (starneig_SEP_DM_Hessenberg(), starneig_SEP_DM_Reduce(), starneig_GEP_DM_HessenbergTriangular(), and starneig_GEP_DM_Reduce()) are wrappers for / use several ScaLAPACK subroutines. The involved matrices should thus be distributed in square blocks. In addition, the ScaLAPACK subroutines usually perform better when the block size is relatively small. The library will automatically convert the matrices to a compatible format but this requires extra memory.

Copy, scatter and gather

An entire distributed matrix can be copied with the starneig_distr_matrix_copy() interface function:

starneig_distr_matrix_t dA, dB;
...
starneig_distr_matrix_copy(dB, dA);

This copies distributed matrix dB to a distributed matrix dA. A region (submatrix) of a distributed matrix can be copied to a second distributed matrix using the starneig_distr_matrix_copy_region() interface function.

A local matrix can be converted to a "single owner" distributed matrix with the starneig_distr_matrix_create_local() interface function:

int owner = 0; // MPI rank that owns the local matrix
double *A;     // local pointer
int ldA;       // matching leading dimension
...
starneig_distr_matrix_t lA = starneig_distr_matrix_create_local(
    n, n, STARNEIG_REAL_DOUBLE, owner, A, ldA);

This creates a wrapper object, i.e., the pointer A and the distributed matrix lA point to the same data on the owner node. The created distributed matrix is associated with a data distribution that indicated that the whole matrix is owned by the node owner. The used block size is 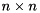$n \times n$ .

Copying from a "single owner" distributed matrix to a distributed matrix performs a scatter operation and copying from a distributed matrix to a "single owner" distributed matrix performs a gather operation.

ScaLAPACK compatibility layer

The library provides a ScaLAPACK compatibility layer:

BLACS contexts are encapsulated inside starneig_blacs_context_t objects.
BLACS descriptors are encapsulated inside starneig_blacs_descr_t objects.

A two-dimensional block cyclic data distribution can be converted to a BLACS context and vice versa using the starneig_distr_to_blacs_context() and starneig_blacs_context_to_distr() interface functions, respectively. Similarly, a distributed matrix that uses a two-dimensional block cyclic data distribution can be converted to a BLACS descriptor (and a local buffer) and vice versa using the starneig_distr_matrix_to_blacs_descr() and starneig_blacs_descr_to_distr_matrix() interface functions, respectively. The conversion is performed in-place and a user is allowed to mix StarNEig interface functions with ScaLAPACK style subroutines/functions without reconversion.

For example,

starneig_distr_matrix_t dA = starneig_distr_matrix_create(...);
...
// convert the data distribution to a BLACS context
starneig_distr_t distr = starneig_distr_matrix_get_distr(A);
starneig_blacs_context_t context = starneig_distr_to_blacs_context(distr);
// convert the distributed matrix to a BLACS descriptor and a local buffer
starneig_blacs_descr_t descr_a;
double *local_a;
starneig_distr_matrix_to_blacs_descr(dA, context, &descr_a, (void **)&local_a);
...
// a ScaLAPACK subroutine for reducing general distributed matrix to upper
// Hessenberg form
extern void pdgehrd_(int const *, int const *, int const *, double *,
    int const *, int const *, starneig_blacs_descr_t const *, double *,
    double *, int const *, int *);
pdgehrd_(&n, &ilo, &ihi, local_a, &ia, &ja, &descr_a, tau, ...);

converts a distributed matrix dA to a BLACS descriptor descr_a and a local pointer local_a. The descriptor and the local array are then fed to a ScaLAPACK subroutine. A user must make sure that the live time of the distributed matrix dA is at least as long as the live time of the matching BLACS descriptor descr_a. See modules ScaLAPACK compatibility / BLACS helpers and ScaLAPACK compatibility / BLACS matrices for further information.